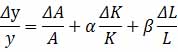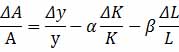近代开滦煤矿产出的“Solow余值”分析

　　【内容提要】近代开滦煤矿企业档案中留存的自20世纪以来完整而连续的生产经营数据，不仅能形成精确的经济统计，也使一些数量关系的分析成为可能。本文应用计量经济学工具方法，建立了自1905年至1936年开滦煤矿产出关于资本、劳动投入的生产模型，同时借用现代经济学理论中“Solow余值”的分析框架，探讨了开滦煤矿生产经营背后的实际因素。

　　【关键词】开滦煤矿；生产函数；Solow余值

一、相关背景与研究思路

　　中国近代历史上的开滦煤矿是中英合资的大型煤矿企业，系河北开平煤矿和滦州煤矿的合称。开滦煤矿的前身为1878年清政府洋务运动中创办的官督商办企业“开平矿务局”，——开平矿务局经营卓有成效，为当时所办新式煤矿中成功之代表，但不幸于1900年庚子国变时落入英商之手成为英资煤矿；滦州煤矿为1907年招集民族资本创办，原为试图收回开平而设，但终于在与开平的竞争中失利，为开平所并。1912年二矿实行名义上的联合，称“开滦矿务总局”，实际为英商掌控；1934年进一步合并，正式成为合资煤矿，人们通常简称其为开滦煤矿。[①]

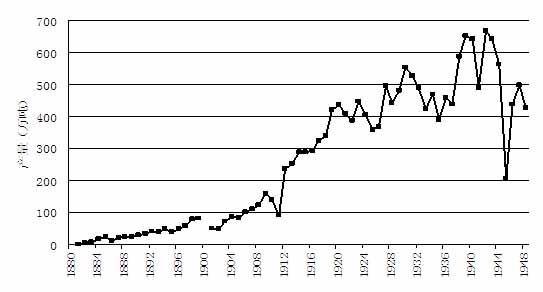
　　开滦煤矿是中国近代煤矿业中的巨擎。从1881年开平矿务局之唐山矿开始出煤至1923年，它的产量一直是全国之冠，1923年以后，辽宁抚顺煤矿（日资）产量开始超过开滦，成为全国产额最巨之煤矿。然而这并不影响开滦矿的重要地位。从纵向看，开滦历整个近代一直连续不断的出煤，产量一直是扩充之势[②]，长期以来供应着天津、上海等多个城市和地区的工业生产和生活用煤，而同期或更早开办的煤矿鲜有能够如此“长盛不衰”者[③]；从横向看，开滦煤矿规模庞大，其资本、技术装备、工人人数在全国首屈一指，优势极为明显，并且煤质较好[④]，国内除抚顺以外的其它大型煤矿实力明显不敌开滦[⑤]。

图1　开滦煤矿产量趋势（1881~1948）

　　资料来源：根据《开滦煤矿志》（第二卷）数字汇总

表1　中国近代各主要煤矿情形（20世纪30年代）

矿名	资本（万元）	工人数量（人）	全年产量（吨）	产煤能力（万吨/年）	资本性质
河北 开滦煤矿	200万英磅[6]	40 985	4 283 999	600	中英
井陉煤矿	450	4 200	706 081	80	中德（德1/4）
正丰公司	660	1500	302 694	40	中国商办
门头沟公司	20万两	2 640	300 200	40	中英
柳江公司	144	952	157 000	30	中国商办
山东 鲁大煤矿	1 000（实收250）	6 200	765 566	80	中日
中兴煤矿	1 000（实收750）[7]	6 940	1 132 544	120	中国商办
山西 保晋公司	286	3 639	432 794	60	中国商办
江苏 华东公司	160	1 280	219 733	25	中国商办
浙江 长兴公司	300	3 200	197 786	20	中国商办
江西 萍乡煤矿	1 000	2 427	172 874	80	中国官办
河南 中福两公司联合办事处	100〔中51英49〕	10 282	1 138 697	160	中英
六河沟公司	600	3 150	519 557	80	中国商办
辽宁 抚顺煤矿	2 000万日金		7 106 558	1 000	南满铁道会社
本溪湖煤矿	700		612 000	70	中日合办

　　资料来源：根据侯德封《中国矿业纪要（第五次）》“第四十八表 民国廿二年中国本部各大矿出产情形”、“第五十七表 东北四省主要煤矿产煤能力表”，“一 煤 （六）矿工”（第106-8页）汇总。（实业部地质调查所、国立北平研究院地质学研究所印行，中华民国24年12月）

　　说明：（1）本表对主要煤矿的选择主要以“全年产量”为标准，排名在前者择入表内。

　　　　　（2）“资本”为注册资本数，“全年产量”为1933年数字，“工人数量”为1933、1934年数字。

　　关于开滦煤矿的研究，自近代已经开始，一直延续至今。然而时代不同，关注侧重有所不同，由此形成经济史、企业史、中外关系史、工运史等诸多方面的研究成果，基本上集中于历史沿革、工人问题和生产经营三大主题。这里限于文章篇幅和主题，不能系统回顾。仅从经济史研究的角度，20世纪60年代，南开大学经济研究所经济史组成员曾赴开滦搜集和整理了围绕矿权演变的资料，以此为基础产生了一些研究成果[⑧]；80年代改革开放，开始注意考察开滦作为一个企业经营实体的经济行为和相关市场运行，于是有一系列涉及生产销售、企业经营管理及中外经济关系的文章[⑨]。又从研究方法的角度，由于开滦煤矿内部保存有自20世纪以来的企业档案，内含连续完整的数据资料，使得现代经济学中的一些工具方法得以应用，从而突破了传统的叙述和定性研究方法。在这方面，南开大学王玉茹曾运用古典经济学资本有机构成理论分析了资本与劳动在开滦煤矿生产中的配置组合，进行了相应的复相关系数测定，开数量分析之先河。后来，梁华、张晓峒使用计量经济学方法，建立了以销售量和吨煤售价为自变量、以公司利润为因变量的函数关系模型，分析开滦煤矿利润的影响因素。

　　数量分析有助于弥补经验认识的不足或检验已有的判断。如在王玉茹的研究中，通过对开滦历年总成本、不变资本与可变资本之比（即资本有机构成）、工资成本、吨煤平均售价等数据进行的复相关系数测定，认为“特权”（主要体现为运价和税负的低廉）只是在某一时期影响开滦的经营效益，而体现生产要素投入组合的资本有机构成和吨煤价格才是决定利润率的主要因素。[⑩]梁华、张晓峒《开滦煤矿利润影响因素的计量分析（1903-1940）》，根据建立的函数关系模型，观察到开滦煤矿利润对吨煤售价的弹性相对较小、对销煤量的弹性则较大，由此通过变动价格获取利润的空间非常小，扩大销煤量是提高利润的重要手段，——这验证了开滦煤矿决策者以扩大销量而非提高售价为经营策略的有效性。

　　本文从研究方法角度，实际上延续了这样一条数量分析的理路。但本文的研究对象并非围绕开滦利润，而是希望通过建立一定历史时期的生产函数模型并进行相应的“Solow余值”测定，在数量上确定不同投入要素对产出的影响，以探讨开滦煤矿该时期内生产过程中发挥作用的实际因素。

　　经济学中常用生产函数表示投入与产出间的数量关系，在新古典经济学理论中，资本和劳动是两个最主要的生产要素，一般用Y=F（K，L）表示，其中Y代表产出，K和L分别代表资本和劳动的投入。1957年，美国经济学家索洛（Solow, R. M.）指出，经济增长不仅取决于资本和劳动两个生产要素的投入，还取决于技术变化因素，产出量的增长是由资本数量的增长、劳动数量的增长和技术进步共同贡献的结果。索洛进一步提出度量技术进步的总量增长方程，并用其来分析美国1909～1949年的经济增长，得出技术进步对美国1909～1949年的经济增长贡献为87.5％。[11]这一发现正式确立了技术在经济增长中的地位，在经济理论研究中具有划时代的意义。索洛用以衡量技术变动的方法，实际上是以产出增加部份不以资本及劳动的增加来解释的部份为技术变动，此即“Solow余值”的由来；而用“Solow余值”除以产出增长，即为“Solow余值”贡献率。本文的思路，即利用开滦煤矿1905-1936年的生产数据，建立这一时期的生产函数模型，然后计算历年的“Solow余值”及其贡献率，以观察资本、劳动及这一余值历年所发挥的作用。

二、生产函数模型的建立与“Solow余值”的测定

　　按照计量经济学的建模步骤，完整的建模应包括模型的设定、样本数据的收集、模型参数的估计与模型检验四个方面。下面根据这一步骤建模。

　　首先是模型的设定。如前所述，现代经济学中常引用生产函数来描述生产过程中投入的生产要素的某种组合同它的产出量之间的依存关系。生产函数常以Cobb-Douglas幂函数的形式出现[12]，其表达式如下：

[13]

　　在这一函数中，Y代表产出量，K代表资本，L代表劳动；A、α和β都是待估参数，如果有足够的生产数据便可对这些参数进行估计，得到具体的函数形式。从经济意义上讲，α、β为要素的产出弹性，A是固定系数。要素的产出弹性（Elasticity of Output）即，当其他投入要素不变时，该要素增加1%所引起的产出量的变化率。这里即采用这一生产函数形式。

　　第二步是样本收据的收集。上述函数中的产出量、资本、劳动，只能称为“因素”，为建立计量经济学模型，必须选择适当变量来表征这些因素，这里以年产量表征产出量，不变资本数表征资本，矿区工人数表征劳动。[14]其中，资本照其来源本是股本、借入资本、各项公积准备和盈余滚存等各部分组成的总额，由于其中已包含着工资支付（即可变成本），而这将与劳动的投入相重叠，应将其剥除，所以采用直接反映固定资产投入的不变成本数代表资本投入；劳动方面，由于开滦是包含煤炭生产、航运码头、焦炭炼制等在内的多种产业经营[15]，而煤炭生产主要与矿区工人数相对应，所以这里选取矿区工人人数。在时间上，三组数据从可得性角度，皆齐全且连续的年份始于1905年，而1937年中日战争爆发，开滦的生产受时局因素影响增强[16]，故选择1905年至1936年的数据[17]。三组数据见表2所列。

表2　开滦煤矿历年产出、资本与劳动数量（1905～1936）

年份	产出Y（煤产量） 单位：吨	资本K（不变成本） 单位：元	劳动L（矿区工人数） 单位：人
1905	833 680	1 459 150.70	6 854
1906	1 000 202	1 822 376.40	7 771
1907	1 117 570	2 330 030.70	7 954
1908	1 226 069	2 164 773.70	7 918
1909	1 359 502	2 264 021.80	8 441
1910	1 170 165	1 949 012.00	7 055
1911	1 488 941	1 999 092.00	6 843
1912	1 693 196	2 260 575.20	10 308
1913	2 532 166	2 681 007.50	12 922
1914	2 877 498	2 941 896.60	13 591
1915	2 884 976	2 260 301.40	13 266
1916	2 932 109	2 331 627.20	11 901
1917	3 254 018	2 462 673.40	12 347
1918	3 398 375	3 594 315.00	14 427
1919	4 201 888	4 283 300.60	17 013
1920	4 363 899	5 592 523.30	19 062
1921	4 085 510	6 974 780.80	19 204
1922	3 874 975	5 902 456.10	19 785
1923	4 464 814	7 484 039.50	22 336
1924	4 024 850	4 627 655.70	23 377
1925	3 581 714	3 681 593.10	23 398
1926	3 683 299	5 207 649.10	21 326
1927	4 958 368	6 348 191.20	25 411
1928	4 414 592	6 543 066.20	24 117
1929	4 812 718	7 781 976.20	26 272
1930	5 541 802	9 241 908.10	29 462
1931	5 262 311	9 465 328.30	30 055
1932	4 874 540	8 779 472.80	29 295
1933	4 223 022	7 916 763.70	29 015
1934	4 699 000	8 124 852.20	33 183
1935	3 898 000	6 235 326.60	26 864
1936	4 590 346	7 539 666.20	31 747

　　资料来源：（1）煤产量，自《开滦煤矿志》第二卷，开滦矿务局史志办公室编，新华出版社，1995年，第311－314页。（2）不变成本，自王玉茹《开滦煤矿的经营效益分析1903/04—1936/37》“表1 开滦煤矿历年总成本及组成变化 （1904/05—1936/37）”，《中国经济史研究》1993年第4期，具体计算情形参见原文说明。（3）矿区工人人数，自《开滦煤矿志》第三卷，第137、139页。

　　第三步是模型参数的估计。先将上文的生产函数等式两边取对数，转化成线性方程[18]，即

　　根据上述线性方程，建立计量模型，如下：

　　再应用计量经济学软件Eviews5.0对上述模型进行回归，软件的输出结果如下：

Dependent Variable: OUT
Method: Least Squares
Sample: 1905 1936
Included observations: 32
Variable	Coefficient	Std. Error	t-Statistic	Prob.
C	5.019539	1.182976	4.243145	0.0002
CAP	0.017255	0.193857	0.089009	0.9297
LAB	0.990824	0.217437	4.556830	0.0001
R-squared	0.873645	Mean dependent var		14.89902
Adjusted R-squared	0.864931	S.D. dependent var		0.563795
S.E. of regression	0.207204	Akaike info criterion		-0.221164
Sum squared resid	1.245074	Schwarz criterion		-0.083751
Log likelihood	6.538621	F-statistic		100.2562
Durbin-Watson stat	0.286696	Prob(F-statistic)		0.000000

　　第四步是进行模型检验。在进行计量经济学模型的回归分析时，必须对所研究对象是否满足普通最小二乘法（OLS）下的基本假定进行检验，这种检验称计量经济学检验。如果检验发现存在违背基本假定的情况，则不能直接使用普通最小二乘法进行参数估计，而必须采取补救措施或发展新的估计方法。根据上表，D-W统计量为0.29[19]，表明模型存在严重的一阶序列自相关性。[20]计量经济学模型一旦出现序列相关性，如果仍采用最小二乘法（OLS）法估计，会出现许多不良后果，如：参数估计量非有效，变量显著性检验失去意义等。这里采取广义差分法对此进行补救，以克服序列相关性对模型的影响。[21]

　　再次应用软件Eview5.0进行回归，输出结果如下：

Dependent Variable: OUT
Method: Least Squares
Sample (adjusted): 1906 1936
Included observations: 31 after adjustments
Convergence achieved after 11 iterations
Variable	Coefficient	Std. Error	t-Statistic	Prob.
C	6.746765	1.598144	4.221624	0.0002
CAP	0.211344	0.102118	2.069604	0.0482
LAB	0.519312	0.156107	3.326650	0.0025
AR(1)	0.829202	0.073260	11.31863	0.0000
R-squared	0.972279	Mean dependent var		14.93984
Adjusted R-squared	0.969199	S.D. dependent var		0.522840
S.E. of regression	0.091760	Akaike info criterion		-1.819370
Sum squared resid	0.227336	Schwarz criterion		-1.634340
Log likelihood	32.20024	F-statistic		315.6634
Durbin-Watson stat	2.439924	Prob(F-statistic)		0.000000
Inverted AR Roots	.83

Dependent Variable: OUT
Method: Least Squares
Sample (adjusted): 1907 1936
Included observations: 30 after adjustments
Convergence achieved after 25 iterations
Variable	Coefficient	Std. Error	t-Statistic	Prob.
C	7.094582	1.612207	4.400539	0.0002
CAP	0.206420	0.100957	2.044638	0.0516
LAB	0.493869	0.154996	3.186327	0.0038
AR(1)	0.597153	0.193946	3.078963	0.0050
AR(2)	0.208404	0.178265	1.169070	0.2534
R-squared	0.969199	Mean dependent var		14.97731
Adjusted R-squared	0.964271	S.D. dependent var		0.487608
S.E. of regression	0.092168	Akaike info criterion		-1.779401
Sum squared resid	0.212372	Schwarz criterion		-1.545868
Log likelihood	31.69102	F-statistic		196.6684
Durbin-Watson stat	1.909970	Prob(F-statistic)		0.000000
Inverted AR Roots	.84	-.25

　　对上面两个结果进行比较，选取前一个结果。由此，得出α=0.211，β=0.519，即资本、劳动的产出弹性分别为0.211和0.519，因此具体的生产函数模型为Y=AK0.211L0.519

　　现在已经得出开滦在这一时期的具体生产函数模型，接下来可以进行“Solow余值”及其贡献率的计算。

　　索洛将技术因素引入生产函数后，进而提出了用总量生产函数度量技术进步的总量增长方程，他认为产出量的增长是由资本数量的增长、劳动数量的增长和技术进步共同贡献的结果。[22]用数学表达式表示即：

　　其中，α和β分别为资本和劳动的产出弹性，式中后两项分别表示资本数量的增长和劳动数量的增长对产出的贡献；ΔA /A是余项，被用来度量技术进步对产出增长的贡献。

　　将开滦历年的产出、资本、劳动的数据代入方程，计算相应年份的ΔA /A，即“Solow余值”，计算公式为：

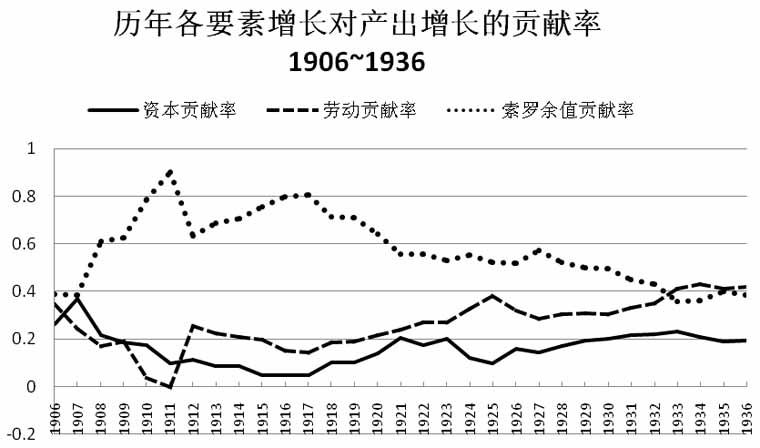
　　其中，α、β已知，Δy/y、ΔK/K、ΔL/L皆是以1905年为基期的各自的增长幅度。同时，也将历年资本数量的增长贡献（α×ΔK/K）和劳动数量的增长贡献（β×ΔL/L）计算出来，与“Solow余值”同除以总量增长（ΔY/Y），得出资本、劳动、“Solow余值”各自的贡献率（如表3所显示）。将表3绘制成图，如图2所显。

表3　历年资本、劳动、“索洛余值”增长对总产出增长贡献率（1906～1936）

年份	资本贡献率 α（ΔK/K）/（ΔY/Y）	劳动贡献率 β（ΔL/L）/（ΔY/Y）	“索洛余值”贡献率 （ΔA /A）/（ΔY/Y）
1906	0.26339	0.34784	0.38877
1907	0.37042	0.24475	0.38483
1908	0.21714	0.17128	0.61158
1909	0.18483	0.19064	0.62452
1910	0.17579	0.03773	0.78648
1911	0.09950	-0.00106	0.90156
1912	0.11259	0.25384	0.63358
1913	0.08687	0.22567	0.68747
1914	0.08760	0.20821	0.70419
1915	0.04716	0.19745	0.75539
1916	0.05021	0.15192	0.79787
1917	0.05007	0.14336	0.80658
1918	0.10053	0.18652	0.71296
1919	0.10125	0.19052	0.70824
1920	0.14138	0.21844	0.64018
1921	0.20481	0.23990	0.55529
1922	0.17642	0.26857	0.55501
1923	0.20035	0.26932	0.53033
1924	0.11989	0.32706	0.55305
1925	0.09766	0.38028	0.52207
1926	0.15884	0.32079	0.52037
1927	0.14313	0.28418	0.57269
1928	0.17143	0.30451	0.52405
1929	0.19188	0.30825	0.49987
1930	0.19961	0.30332	0.49708
1931	0.21830	0.33092	0.45079
1932	0.21875	0.35079	0.43046
1933	0.23006	0.41301	0.35693
1934	0.20823	0.43026	0.36151
1935	0.18821	0.41247	0.39932
1936	0.19546	0.41860	0.38594
平均	0.16167	0.26224	0.57609

图2 资本、劳动与“Solow余值”对开滦煤矿产出增长的贡献率（1906～1936）

三、对“Solow余值”及其贡献率的解读

　　表3和图3的示意结果，可说超乎意料。一般从经验认识里，投入越大，则产出越大，可是根据这里的结果，资本和劳动作为生产中最主要的要素投入，却不能同样“最主要”地解释产出的增长。从1906～1936三十年间，“Solow余值”的贡献率长期超过劳动与资本的贡献率。三者平均贡献率分别为：资本16.2％，劳动26.2％，“Solow余值”57.6％。这似乎说明开滦长期以来的产出增长主要不是来自资本和劳动的贡献，而是“Solow余值”贡献的结果。

　　“Solow余值”按照索洛的本意，是用来度量技术进步对产出增长的贡献，但从计算的角度，这一余项实际上是从产出变动中扣除由于资本及劳动的影响所剩余的部份，亦即产出增长中不能被资本、劳动数量的增长所解释的部分。实际上，余值是否可以惟一的为技术进步所解释，是个存疑的问题。而除了技术进步因素外，组织效率的改进，管理水平的提高，规模经济效应以及新产品的开发、新工艺的发明等等，都有可能对产出增长形成影响而涵括在这一余项中。随着经济学理论的发展，索洛用以示意技术进步的“余值”内涵也向广义延伸，终于发展到今天经常使用的“全要素生产率（TEP）”概念[23]。而这里需要阐明的是，本文对“Solow余值”一开始即作广义理解，即不以技术进步为对“Solow余值”惟一甚至主要的解释。

　　实际上，就开滦的技术进步而言，如果以人均采煤效率衡量，中国近代煤矿的平均每工采煤效率为0.65吨[24]，开滦大致上1912/13年度为1.09吨，1936/37年度为1.26吨，[25]——虽远高于平均水平，但从自身发展上看提高缓慢，甚至1937年后还有不足1吨的情况[26]，可见技术进步速度并不快。

　　那么，如果不是技术进步，究竟是什么原因造成了“Solow余值”贡献率的高值，从长期看，又是什么原因造成资本、劳动、“Solow余值”各自贡献率的涨落？这需要结合经验观察来分析。

　　首先，从1906年至1917年，“Solow余值”的贡献率一直处于上升状态[27]。考察这一时期开滦的经历，英国人入主开平后进行了制度上的“外科手术”，包括裁汰冗员、改革机构等，使之成为现代意义上的西方式经营管理企业。此前的“开平矿务局”，虽然是众多洋务新式企业中卓有成效者，但是管理人员以办矿为做官，致使人浮于事、营私舞弊、虚靡浪费、层层揩油。据1887年6月24日《北华捷报》的一篇报导，“当开平矿山正在欣欣向荣、继续发展的时候，所有督办、总办和其它大员的三亲六戚都成群结队而来。而且完全不管他们能否胜任，都一律委以差使，把他们养得肥肥的”[28]。这种情况到英人占据前更为严重，——1901年出任开平公司总工程师的胡华（即赫伯特·胡佛，美国第31届总统）发现，工薪单上竟虚报了6000个名额，而掌管该事的职位是以5万元购得的[29]；胡华在“开平矿务公司报告”（1900年）中还曾反映“公司采用中式记帐，既不能用来、也不打算说明成本。所列出的各项费用除表示可能达到的最大数额外，也没有什么价值”[30]。可见，开平煤矿在被英人占据之前，经营上存在很大的问题。1900年开平煤矿的丧失，除了矿权易手外，最重大的变化是企业制度上的变革，而这一变革不可能对其产出效率毫无影响。1912年二矿联合后，经营上又有调整，同时又集中了最先进的生产设备。所有这些因素作用于产出上，都形成了“Solow余值”贡献率的涨高。

　　从1917年至1936年，余值贡献率逐渐呈下降态势，而资本和劳动贡献率则相应呈增长趋势，并且劳动贡献率甚至在1932年开始超过“Solow余值”的贡献率。考察这一时期的历史，企业制度较先前已无重大变革，企业规模也基本稳定下来[31]，基于组织效率和管理水平提高而形成的生产改善，以及二矿联合后所产生的规模经济效果等，已不再能对产出增加持续发挥效果。另一方面，开滦虽然在技术实力上始终处于一流，但与从前相比，已不再有绝对优势，特别在技术更新上，有时反不如其它煤矿主动。比如，近代首先应用割煤机采煤的是中兴煤矿，而第一个购买割煤机的是保晋公司阳泉煤矿[32]；再如，萍乡煤矿早在1907年用上了电机车进行井下运输[33]，而开滦煤矿在井下大巷使用电机车则始于1929年[34]。由此，这一时期“Solow余值”的贡献效果开始日益不显著。

　　最后，就资本与劳动的比较而言，1911年以前，资本要素的贡献率高于劳动的贡献率，从1912年开始，劳动贡献率开始超过并长期高于资本贡献率，——这可以与经验观察互为参证。1908/09年度的总经理年报中说：“设备的生产能力超过了现在的需要，但随着产量的进一步增长，……这一不足之处即将归于消灭”[35]。事实上，在技术设备已能充分发挥功用后，英人更倾向劳动的使用，并且发展到后来越来越偏重于劳动的投入，前文采煤效率的例子也说明开滦后来并不主要依赖设备的投入或机械化来提高总煤产。究其原因，正如开滦总经理杨嘉立（英国人）1930年所说：“无论何项工业莫不以减少雇工为目的，而减工之宗旨实在于减轻成本。今在工价低贱之国，从经济方面而论，实无利用省工机器之必要。”[36]由此，在开滦后期的生产增长中，劳动的贡献率较大。

四、对几个问题的“回应”和思考

　　本文的研究在成果展示过程中，曾受到来自多方面的意见，下面就几个主要问题进行“回应”。

　　首先是“Solow余值”的适用性问题。在现代经济学中，“Solow余值”经常被用于宏观经济分析中，而本文却将之运用于微观分析，由此产生适用性的疑问。其实对于“Solow余值”法在社会总生产问题上的有效性方面，笔者心存疑问，主要理由在于其生产函数型式的设定假设上，——总生产函数显然采用了柯布-道格拉斯生产函数型式，但社会总生产五花八门，既包括农业、工业等不同类型的生产，也存在跨国生产和世界性分工体系等诸多复杂因素，由此社会总生产函数未必与厂商生产函数同型，以此来测度社会全体产出中的技术进步（广义），可能存在巨大误差。而开滦是单个厂商，柯布-道格拉斯生产函数本也是微观生产模型，因此这里认为“Solow余值”方法可以适用。

　　再就是开滦生产模型的建立。生产函数的设定经常会受到质疑，——因为影响产量的因素有很多，不是仅仅关乎资本、劳动等的投入。应该说，同样是建立生产模型，所处的经济环境不同，研究的行业不同，变量选择是不同的。在生产问题中，已经明确属于供给不足的情况，那么影响产出量的因素就应该在投入要素方面，如果属于需求不足的情况，那么影响产出量的因素就应该在需求方面；如果研究的对象是消费品生产，应该选择居民收入等变量作为解释变量，如果研究的对象是生产资料生产，应该选择固定资产投资总额等变量作为解释变量。[37]就开滦的企业性质和在近代生产的具体情况来说，认为大致符合供给不足的生产资料型生产，因此采用了上文所见的变量选择和模型型式。

　　另一个经常被问及的问题是，资本投入中已内含生产设备的投入，而生产设备正包含技术进步，那么资本的贡献实际上不就与“Solow余值”的贡献重合了吗？这是一个比较难回答的问题。就笔者自己的理解，索洛为衡量技术进步在经济增长中的贡献而采用的余值法，意在考察一种长期内客观的、社会普遍意义上的技术进步，这种技术进步[38]反映出来的是一种效果；资本投入中的技术进步是在当期一定技术水平上投入的该技术的使用量，与“Solow余值”中的技术进步实际上是异质的。因此，这是技术投入所产生的与技术进步带来的两种性质不同的贡献。

　　计量经济学工具方法在历史研究领域中的应用无疑是有风险和挑战性的，它应用的有效或成功与否很大程度上取决于是否与事实经验相吻合。本文所作的尝试，其结果与经验观察不悖，说明不失有效性。在此基础上，遂引发对于一些问题和认识的再思考。

　　近代时期，国人对于开滦煤矿有不胜惋惜之情。由于它本为中国人自己开办的煤矿，后来落入外人之手，几次交涉收回都未能成功，只能坐视滚滚利润外流，每每产生“利权外溢”之感慨，同时又有诸如“英商开平以合滦矿而存”等之说[39]。由中华矿学社主办的《矿业周报》载有一篇“商民协会电请发展国煤”，可以看出民族资本要求利权、维护利源意愿的强烈：

　　“……北伐成功，建设伊始，奖掖工商，急不容缓，最要问题尤在于煤……历年以来，煤权操诸外商，估计损失，年达一万万元……

　　“又有进者，滦州煤矿公司，前因利用开平轮埠，遂与开平商订合作契约，缔约而后，叠年采运，达四百万吨，值价四千万元，是项矿权，全操于外人之手，……开平矿量，业已告罄，利用滦矿订约，始能操纵自如……”[40]

　　后来的研究者亦多籍类似文献并延此思路，强调帝国主义在华势力及对民族经济之形成掠夺和压制。笔者以为，主张利权，无论在当时还是从今天看，不仅必要而且必需。然而，“摘去”外因，仍有内因；不见内因，主张利权则易失真正鹄的。1928年天津《益世报》对开滦曾有一段报道，

　　“开滦为我国东北矿业之冠，祗以主权操之于英，故出产如何，工人生活如何，为帝国主义所把持，国人概难深知，为明了真相计，记者特亲赴开滦矿区实地调查，见其规模宏大，出产之丰富，不胜利权外溢之感，……而矿内不知有何秘密，英国人禁止参观，殊深怅恨……”[41]

　　其实，无缘参观开滦矿内的记者在深感遗憾的同时，倒向我们形象的展示出一幅企业生产的“外征”，——“规模庞大”显其投入，“出产丰富”示其结果，这些都是显而易见的，而关键与“秘密”处正在于从投入到产出的这一中间过程；如果将庞大先进的设备、规模众多的矿工视为企业生产的“硬件”，则在这一中间过程中，发挥作用的是不那么易见和外显的“软件”，同时也正是本文“Solow余值”的贡献所在。

　　事实上，国内其它一些煤矿的发展经历也验证了资本与劳动的投入并非增长的实际因素。江西萍乡煤矿，曾为我国自办各矿中资本最大、规模最备者[42]，年产能力不让井陉、鲁大等中外合资大煤矿，并且在采用最先进技术上不遗余力，——西方煤矿大约于20世纪初大量使用电机车来取代骡马进行井下运输，而大致同时，萍乡煤矿也用上了电机车——1907年在总平巷使用架线式电机车[43]，同年安装的洗选设备据说不仅开平煤矿当时没有，就是在亚洲也不多见[44]。然而除了经历过一战时期的短暂繁荣外，却是后来每况愈下，几乎逐年减产。足见庞大的投资、一流的设备并不能保证产出的增长。

　　由此观之，在处理近代外资与民族资本之间的矛盾问题上，无论对当时代人还是今人而言，只看到前者侵夺、恃强的一面，最终只能陷入一种肤浅的民族主义。本文以开滦煤矿为例的“Solow余值”法分析，可藉省视的是，资本和劳动这些“硬件”的投入绝非增长的决定力量，只有将智慧和力量集中于“软件”，才是民族资本获得长足发展和实质进步的关键。

注释：

※ 本文感谢清华大学人文学院陈争平教授在思路上的最初点拨和指导，同时感谢清华大学博士研究生常旭在应用计量经济学及软件包Eviews方面的协助，亦感谢英国谢菲尔德大学Tim Wright教授、南开大学王玉茹教授（惠赐1988年硕士论文）、中国社会科学院经济所刘兰兮老师、近代史所史建云老师等在研究成果展示过程中提出的宝贵意见。

[①] 关于开滦煤矿的历史，自近代始有研究，以杨鲁之专著《开滦矿历史及收归国有问题》（1932）为代表；建国以后，魏子初之《帝国主义与开滦煤矿》（1954）在导言中对开滦历史有较为清晰的论述；此外，台湾中央研究院王玺著有《中英开平矿权交涉》（1962），对开滦矿的历史沿革叙述较为完整，可资参考。

[②] 参加本文图1“开滦煤矿产量趋势（1881~1948）”。

[③] 例如，台湾基隆煤矿（1876年建）因长期亏蚀于1892年封闭，湖北荆门煤矿（1879年建）因资本短缺于1882年停办，山东峄县煤矿（1880年建）于1895年因大水而禁采，广西富川贺县煤矿（1880年建）因煤质较差、运输困难于1886年闭歇等等。关于中国近代早期兴办之新式煤矿情形，参见《中国近代煤矿史》，煤炭工业出版社1990年版，第19、40-2页；严中平等编《中国近代经济史统计资料选辑》，科学出版社1955年版，第96-7页。

[④] 开滦煤矿的煤种为古生代中变质的烟煤，煤质属中级。就近代全国煤矿整体水平看，开滦煤质居于中上地位，——辽宁抚顺煤矿虽年产量后来跃过开滦，但煤质属“褐性烟炭”，显然低于开滦。当时代人胡荣铨在《中国煤矿》（1935）一书中即评价说，“开平煤田，质量均佳。煤系烟煤，燃烧时发长焰。极适于火车、轮船，及制铁等之用。”

[⑤] 参见本文表1“中国近代各主要煤矿情形（20世纪30年代）”。

[⑥] 如果照1932年英镑与国币比价1:16计算，合国币3 200万元，——比价据《矿业周报》第219号“开平中原两公司二十年度之盈余比较”一文（中华民国21年12月21日印行）。

[⑦] 又据《矿业周报》第一集（中华矿学社1928年出版载），资本750万元（财产价值1 400万元）。

[⑧] 代表如熊性美《论英国资本对开滦煤矿经营的控制——开滦矿权丧失的原因分析之一》（1963年脱稿，发表于《南开经济研究所季刊》1986年第2期）。

[⑨] 如张国辉《从开滦煤矿联营看近代煤矿业发展状况》，刘佛丁《开平矿务局经营得失辨析》，丁长清《从开滦看旧中国煤矿业中的竞争和垄断》、《开滦煤矿在旧中国市场上的运销初析》、《开滦煤矿人事管理的历史考察》等。

[⑩] 参见王玉茹《开滦煤矿的经营效益分析1903/04—1936/37》，《中国经济史研究》1993年第4期。另一篇相关的文章为《开滦煤矿的资本集成和利润水平的变动》，对开滦历年的资本利润率、股息率和成本利润率等做了计算，给出了开滦资本集成和利润水平的变动趋势，见《近代史研究》，1989年第4期。

[11] 罗伯特·M·索洛等著：《经济增长因素分析》，商务印书馆1991年版，第19页。

[12] 20世纪20年代末，美国数学家Charles Cobb和经济学家Paul Dauglas用1899~1922年的数据资料，导出了这一形式的函数，此即著名的柯布-道格拉斯（Cobb-Dauglas）生产函数。

[13] 原始型式为Q=a0La1Ka2，文中式为当今经济学教科书中普遍采用的表达式。

[14] 煤产量数据来自《开滦煤矿志》第二卷，第311－314页；不变成本，自王玉茹《开滦煤矿的资本集成和经营效益分析》（硕士论文），1988年4月，“表5 开滦煤矿历年总成本及组成变化”，第49页；矿区工人人数，自《开滦煤矿志》第三卷，第137、139页。

[15] 开滦在开平矿务局时代的产业经营芜杂繁多，所属单位大致有三类，一类是煤矿和煤运部门，另一类是码头，再一类是其它产业（如水泥厂和金银矿等）；1912年开滦合并后，业务始渐集中于煤炭生产，且越到后期越趋集中。

[16] 特别1941年太平洋战争爆发、日本占领了开滦煤矿实行军管理后，开滦煤矿已在非正常情况下生产。

[17] 另外，会计年度上，1901年至1902年的会计年度系自1901年2月19日至1902年2月底；1902～1912年会计年度系3月1日至下年2月底；1912～1940年会计年度系7月1日至下年6月30日，这里皆以会计年度起始月份所在年计当年产量。

[18] 转化成线性方程的目的是可利用最小二乘法（OLS）进行回归对参数进行估计，这一过程可以通过计量经济学软件完成。

[19] D-W统计量是杜宾（J. Durbin）和瓦森（G.S. Watson）于1951年提出的一种检验序列自相关的方法。在检验时，须计算该统计量的值，再根据样本容量n和解释变量数目k查D.W.分布表，得到临界值dL和dU；如果0

[20] 此外，残差项变化也反映出模型存在序列相关性（图略）。序列相关性意味着模型的随机干扰项违背了相互独立的基本假设；对于采用时间序列数据作样本的计量经济学问题，由于在不同样本点上解释变量以外的其他因素在时间上的连续性，带来它们对被解释变量的影响的连续性，所以往往存在序列相关性。

[21] 广义差分法是一类克服序列相关性的有效方法，被广泛地采用。它是将原模型变换为满足普通最小二乘法的差分模型，再进行普通最小二乘估计。

[22] 见李子奈、潘文卿编著：《计量经济学》，高等教育出版社2005年版,第2版，第231页。

[23] 据林毅夫、任若恩，全要素生产率（TFP, Total Factor Productivity）考虑的是所有的投入要素（劳动、资本等），在经济增长核算理论中全要素生产率是一个“残差”，等于产出增长率与各个被计算到的投入要素增长率加权和之差。——林毅夫、任若恩《东亚经济增长模式相关争论的再探讨》，《经济研究》2007年第8期。

[24] 《矿业周报》（第一集），“机械装煤”，中华矿学社，1928年（民国17年），第305页。

[25] 见郭士浩主编：《旧中国开滦煤矿工人状况》，人民出版社1985年版，第46页。

[26] 1942/43年度为0.87吨，1947年为0.79吨，见郭士浩主编《旧中国开滦煤矿工人状况》，第46页。

[27] 1911年由于劳动贡献率为负值（可能与这一年正当二矿联合前夕而开工不足有关），因此“Solow余值”在本年达到峰值而使整个曲线呈波动状，事实上，如果剔除这一年份，其曲线的上升还是较为平缓的。

[28] 转引自刘佛丁《开平矿务局经营得失辨析》，《南开学报》1986年第2期，第36页。

[29] 《胡华回忆录，冒险的年代，1874－1920年》，纽约麦克米伦1951年版，1：62，转见刘佛丁，《开平矿务局经营得失辨析》，《南开学报》，1986年第2期。

[30] 胡华：《开平矿务公司报告》，见《开滦煤矿矿权史料》，第31页。

[31] 开滦煤矿在近代时期主要有五个矿井出煤，分别为唐山矿、林西矿、马家沟矿、赵各庄矿、唐家庄矿，号称“开滦五矿”，除了唐家庄矿（1920年开凿、1925年出煤）外，其余皆建于1910年前。

[32] 《中国近代煤矿史》，第186页。

[33] 《中国近代煤矿史》，第195页。

[34] 开滦矿务局史志办公室编，《开滦煤矿志（1878－1988）》第二卷，新华出版社1995年版，第174页。

[35] 转引自王玉茹《开滦煤矿的经营效益分析1903/04—1936/37》

[36] 《开滦矿务总局待遇职工状况》，1930年，转见郭士浩主编，《旧中国开滦煤矿工人状况》，人民出版社1985年版，第46页。

[37] 李子奈、潘文卿编著，《计量经济学》（第三版），高等教育出版社2010年版，第10页。

[38] 笔者更愿意采用“效率的改进”。

[39] 《矿业周报》第216号，“本社为福公司事件敬告全国同胞书”，中华矿学社，民国21年11月30日印行，第753页。

[40] “商民协会电请发展国煤（免除特税利便运输 收回开平煤矿”，1928年，见《矿业周报》第一集第十一号，中华矿学社民国十七年八月十四日印行。

[41] 转引自中华矿学社《矿业周报》第一集“唐山煤矿工人困苦”，民国十七年（1928）出版。

[42] 《中国矿业纪要（第二次）》，民国十五年（1926），第35页。

[43] 《中国近代煤矿史》，第195页。

[44] 《中国近代煤矿史》，第208页。

（作者单位：中国社会科学院近代史研究所 100006）